how to find the radius of a circle inscribed in a triangle
Confining and inscribed circles of triangles

Circumscribed and inscribed circles are sketched effectually the circumcenter and the incenter
In this lesson we'll look at circumscribed and inscribed circles and the special relationships that grade from these geometric ideas.

Hello! I'm krista.
I create online courses to assist y'all rock your math class. Read more.
Circumscribed circles
When a circle circumscribes a triangle, the triangle is within the circle and the triangle touches the circle with each vertex.
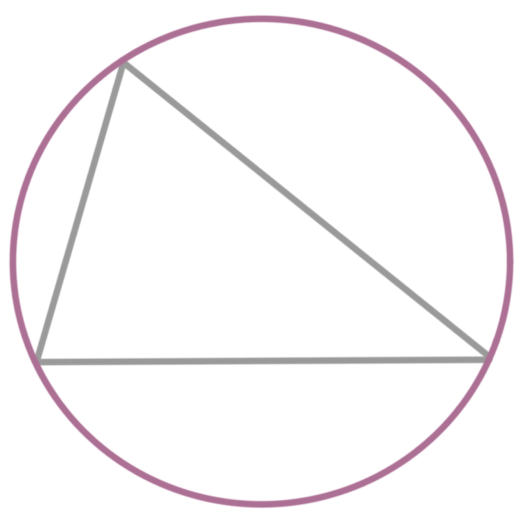
Yous use the perpendicular bisectors of each side of the triangle to find the the center of the circle that will delimit the triangle. And then for example, given ???\triangle GHI???,
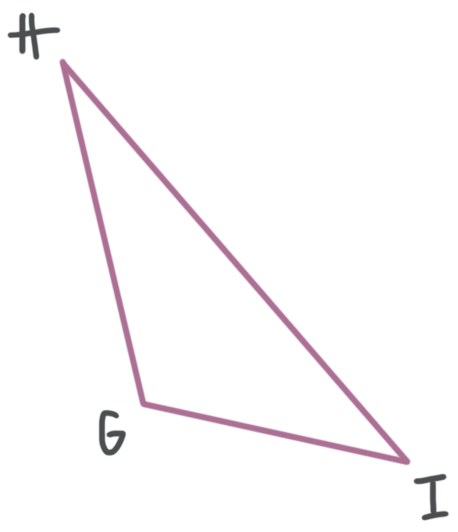
find the midpoint of each side.

Detect the perpendicular bisector through each midpoint.
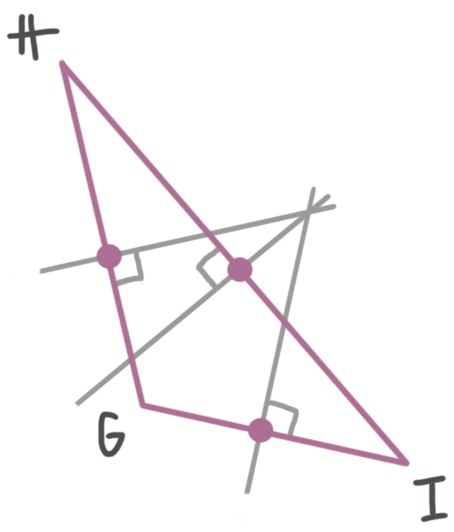
The point where the perpendicular bisectors intersect is the center of the circle.
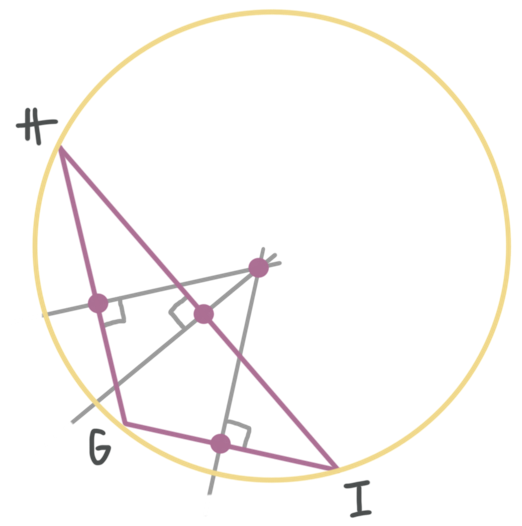
The center point of the circumscribed circle is called the "circumcenter."
-
For an acute triangle, the circumcenter is within the triangle.
-
For a right triangle, the circumcenter is on the side opposite right angle.
-
For an obtuse triangle, the circumcenter is exterior the triangle.
Inscribed circles
When a circumvolve inscribes a triangle, the triangle is exterior of the circle and the circle touches the sides of the triangle at one point on each side. The sides of the triangle are tangent to the circle.
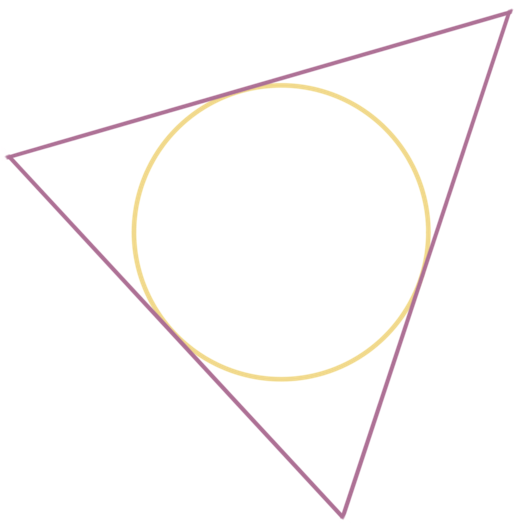
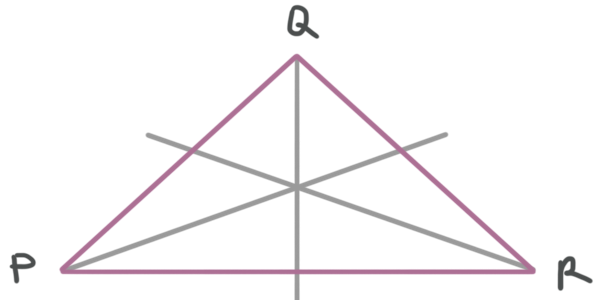
To drawing an inscribed circle inside an isosceles triangle, employ the angle bisectors of each side to discover the center of the circle that's inscribed in the triangle. For instance, given ???\triangle PQR???,

describe in the angle bisectors.
The intersection of the angle bisectors is the center of the inscribed circle.
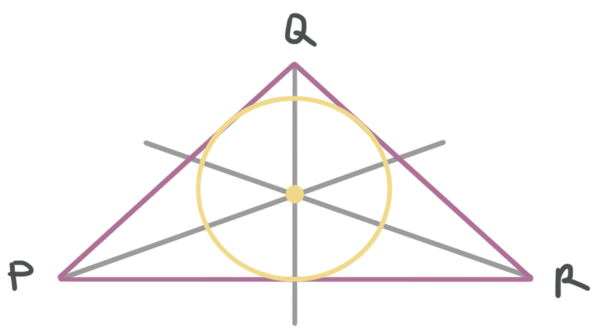
Remember that each side of the triangle is tangent to the circle, so if you draw a radius from the center of the circle to the signal where the circle touches the border of the triangle, the radius volition form a right angle with the border of the triangle.
The center betoken of the inscribed circle is called the "incenter." The incenter will always be within the triangle.
Allow's employ what we know about these constructions to solve a few bug.
Finding and sketching circumscribed and inscribed circles


Take the course
Want to learn more about Geometry? I have a pace-past-step course for that. :)
Finding the radius of the circle that circumscribes a trianle
Example
???\overline{GP}???, ???\overline{EP}???, and ???\overline{FP}??? are the perpendicular bisectors of ???\vartriangle ABC???, and ???AC=24??? units. What is the measure of the radius of the circle that circumscribes ???\triangle ABC????

Point ???P??? is the circumcenter of the circumvolve that circumscribes ???\triangle ABC??? because it'due south where the perpendicular bisectors of the triangle intersect. We tin can draw ???\bigcirc P???.
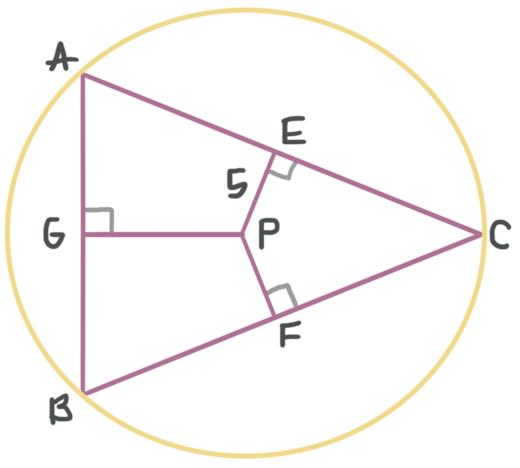
We also know that ???Air conditioning=24??? units, and since ???\overline{EP}??? is a perpendicular bisector of ???\overline{AC}???, point ???East??? is the midpoint. Therefore,
???EC=\frac{1}{2}Air-conditioning=\frac{i}{2}(24)=12???
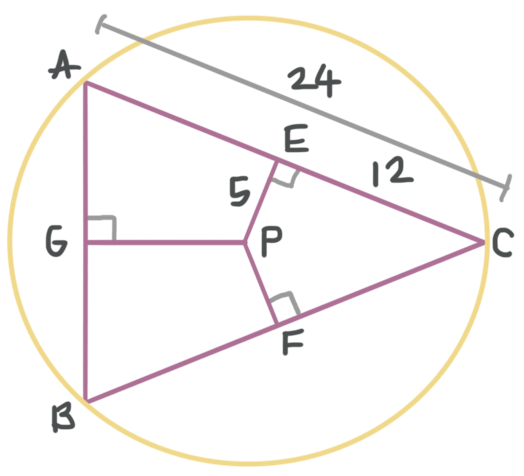
Now we can draw the radius from point ???P???, the centre of the circle, to point ???C???, a signal on its circumference.
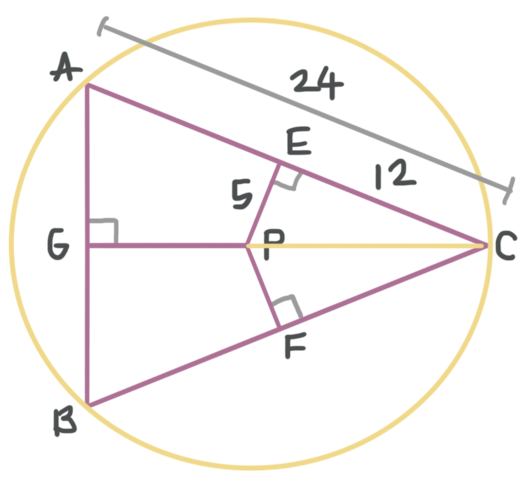
We tin use correct ???\triangle PEC??? and the Pythagorean theorem to solve for the length of radius ???\overline{PC}???.
???{{v}^{ii}}+{{12}^{2}}={{(PC)}^{two}}???
???PC=thirteen???
Allow'south try a different problem.

You use the perpendicular bisectors of each side of the triangle to detect the the center of the circle that will circumscribe the triangle.
Example
If ???CQ=2x-7??? and ???CR=ten+5???, what is the measure of ???CS???, given that ???\overline{Xc}???, ???\overline{YC}???, and ???\overline{ZC}??? are bending bisectors of ???\triangle XYZ???.
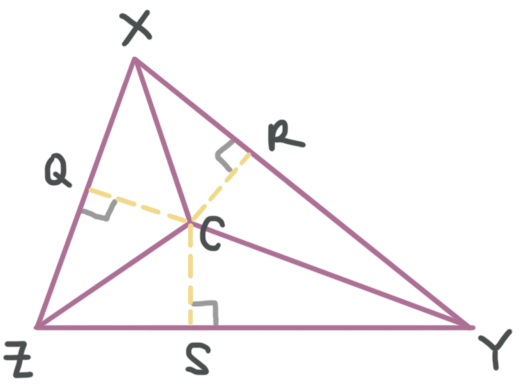
Because ???\overline{XC}???, ???\overline{YC}???, and ???\overline{ZC}??? are angle bisectors of ???\triangle XYZ???, ???C??? is the incenter of the triangle. The circumvolve with center ???C??? will be tangent to each side of the triangle at the point of intersection.
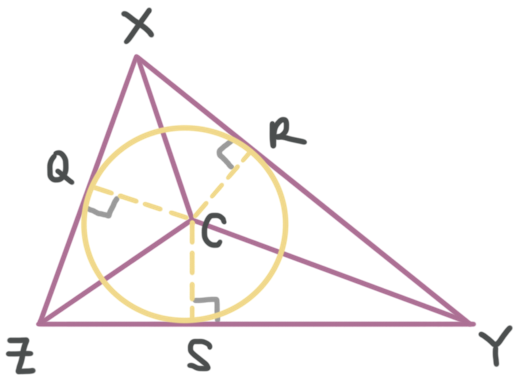
???\overline{CQ}???, ???\overline{CR}???, and ???\overline{CS}??? are all radii of circumvolve ???C???, so they're all equal in length.
???CQ=CR=CS???
We need to find the length of a radius. We know ???CQ=2x-vii??? and ???CR=10+v???, then
???CQ=CR???
???2x-7=x+5???
???x=12???
Therefore,
???CQ=CR=CS=x+5=12+5=17???

Get access to the complete Geometry class
Source: https://www.kristakingmath.com/blog/circumscribed-and-inscribed-circles-of-triangles
Posted by: madsensels1994.blogspot.com

0 Response to "how to find the radius of a circle inscribed in a triangle"
Post a Comment