How To Find The Roots Of A Parabola

Parts of a Parabola

The graph of a quadratic function is a parabola, and its parts provide valuable information about the function.

Learning Objectives

Describe the parts and features of parabolas

Fundamental Takeaways

Key Points

• The graph of a quadratic function is a U-shaped curve called a parabola.
• The sign on the coefficient [latex]a[/latex] of the quadratic part affects whether the graph opens up or down. If [latex]a<0[/latex], the graph makes a frown (opens downward) and if [latex]a>0[/latex] then the graph makes a smiling (opens upwards).
• The extreme betoken ( maximum or minimum ) of a parabola is chosen the vertex, and the axis of symmetry is a vertical line that passes through the vertex.
• The x-intercepts are the points at which the parabola crosses the x-axis. If they exist, the 10-intercepts correspond the zeros, or roots, of the quadratic function.

Central Terms

• vertex: The signal at which a parabola changes management, corresponding to the minimum or maximum value of the quadratic function.
• axis of symmetry: A vertical line drawn through the vertex of a parabola around which the parabola is symmetric.
• zeros: In a given part, the values of [latex]x[/latex] at which [latex]y=0[/latex], besides called roots.

Recall that a quadratic part has the grade

[latex]\displaystyle f(ten)=ax^{two}+bx+c[/latex].

where [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] are constants, and [latex]a\neq 0[/latex].

The graph of a quadratic function is a U-shaped curve chosen a parabola.  This shape is shown beneath.

Parabola : The graph of a quadratic office is a parabola.

In graphs of quadratic functions, the sign on the coefficient [latex]a[/latex] affects whether the graph opens up or downwards. If [latex]a<0[/latex], the graph makes a pout (opens down) and if [latex]a>0[/latex] and so the graph makes a smile (opens up). This is shown below.

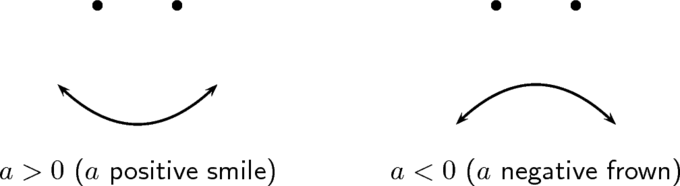
Management of Parabolas: The sign on the coefficient [latex]a[/latex] determines the direction of the parabola.

Features of Parabolas

Parabolas accept several recognizable features that characterize their shape and placement on the Cartesian airplane.

Vertex

One of import characteristic of the parabola is that information technology has an farthermost signal, called the vertex. If the parabola opens up, the vertex represents the lowest signal on the graph, or the minimum value of the quadratic function. If the parabola opens downwardly, the vertex represents the highest betoken on the graph, or the maximum value. In either instance, the vertex is a turning betoken on the graph.

Axis of Symmetry

Parabolas likewise have an axis of symmetry, which is parallel to the y-centrality. The axis of symmetry is a vertical line drawn through the vertex.

[latex]y[/latex]-intercept

The y-intercept is the point at which the parabola crosses the y-axis. There cannot be more than one such bespeak, for the graph of a quadratic function. If there were, the curve would not be a part, equally at that place would be two [latex]y[/latex] values for 1 [latex]10[/latex] value, at nothing.

[latex]x[/latex]-intercepts

The x-intercepts are the points at which the parabola crosses the x-centrality. If they be, the x-intercepts represent the zeros, or roots, of the quadratic office, the values of [latex]x[/latex] at which [latex]y=0[/latex]. At that place may be aught, 1, or 2 [latex]x[/latex]-intercepts. The number of [latex]x[/latex]-intercepts varies depending upon the location of the graph (run across the diagram below).

Possible [latex]10[/latex]-intercepts: A parabola tin have no x-intercepts, one x-intercept, or ii x-intercepts

Recall that if the quadratic function is set equal to zero, then the result is a quadratic equation. The solutions to the equation are called the roots of the function. These are the same roots that are observable equally the [latex]10[/latex]-intercepts of the parabola.

Notice that, for parabolas with two [latex]x[/latex]-intercepts, the vertex always falls between the roots. Due to the fact that parabolas are symmetric, the [latex]x[/latex]-coordinate of the vertex is exactly in the heart of the [latex]x[/latex]-coordinates of the 2 roots.

A Graphical Interpretation of Quadratic Solutions

The roots of a quadratic function can be institute algebraically or graphically.

Learning Objectives

Describe the solutions to a quadratic equation equally the points where the parabola crosses the x-axis

Cardinal Takeaways

Primal Points

• The roots of a quadratic function tin be found algebraically with the quadratic formula, and graphically past making observations nearly its parabola.
• The solutions, or roots, of a given quadratic equation are the same as the zeros, or [latex]x[/latex]-intercepts, of the graph of the corresponding quadratic role.

Primal Terms

• zeros: In a given function, the values of [latex]x[/latex] at which [latex]y = 0[/latex], also called roots.

Recall how the roots of quadratic functions can be found algebraically, using the quadratic formula [latex](x=\frac{-b \pm \sqrt {b^2-4ac}}{2a})[/latex]. The roots of a quadratic function can also be found graphically by making observations nearly its graph. These are two different methods that can be used to reach the aforementioned values, and we will now meet how they are related.

Consider the quadratic function that is graphed below. Allow'south solve for its roots both graphically and algebraically.

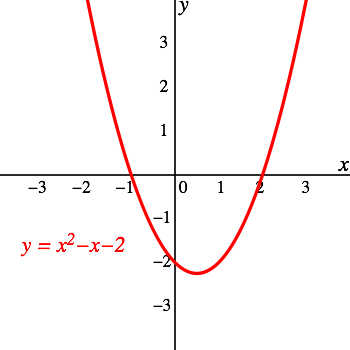
Graph of the quadratic role [latex]f(x) = ten^2 – x – 2[/latex]: Graph showing the parabola on the Cartesian plane, including the points where it crosses the ten-axis.

Notice that the parabola intersects the [latex]x[/latex]-axis at two points: [latex](-1, 0)[/latex] and [latex](2, 0)[/latex]. Think that the [latex]x[/latex]-intercepts of a parabola indicate the roots, or zeros, of the quadratic part. Therefore, there are roots at [latex]x = -1[/latex] and [latex]x = 2[/latex].

Now, let's solve for the roots of [latex]f(x) = x^2 - x- two[/latex] algebraically with the quadratic formula.

Recall that the quadratic equation sets the quadratic expression equal to zero instead of [latex]f(ten)[/latex]:

[latex]0 = x^2 - x - two[/latex]

Now the quadratic formula tin be applied to find the [latex]x[/latex]-values for which this statement is true. For the given equation, we have the following coefficients: [latex]a = 1[/latex], [latex]b = -1[/latex], and [latex]c = -2[/latex].

Substitute these values in the quadratic formula:

[latex]ten = \dfrac{-(-one) \pm \sqrt {(-one)^2-iv(1)(-ii)}}{two(1)}[/latex]

Simplifying, we have:

[latex]ten = \dfrac{1 \pm \sqrt {nine}}{ii} \\[/latex]

and

[latex]ten = \dfrac{1 \pm iii}{2}[/latex]

We now have 2 possible values for x: [latex]\frac{1+3}{ii}[/latex] and [latex]\frac{1-iii}{two}[/latex].

These reduce to [latex]x = two[/latex] and [latex]x = - i[/latex], respectively. Notice that these are the same values that when institute when we solved for roots graphically.

Example

Notice the roots of the quadratic role [latex]f(ten) = x^2 - 4x + 4[/latex]. Solve graphically and algebraically.

The graph of [latex]f(x) = x^2 – 4x + 4[/latex].: The graph of the to a higher place role, with the vertex labeled at [latex](2, one)[/latex].

Looking at the graph of the function, we find that information technology does non intersect the [latex]ten[/latex]-centrality. Therefore, it has no existent roots.

We can verify this algebraically. First, identify the values for the coefficients: [latex]a = 1[/latex], [latex]b = - iv[/latex], and [latex]c = 5[/latex].

Substituting these into the quadratic formula, we have:

[latex]x=\dfrac{-(-four) \pm \sqrt {(-iv)^2-4(i)(v)}}{two(ane)}[/latex]

Simplifying, we take:

[latex]x=\dfrac{4 \pm \sqrt {16-20}}{2} \\ x=\dfrac{4 \pm \sqrt {-4}}{2}[/latex]

Notice that we have [latex]\sqrt{-4}[/latex] in the formula, which is not a existent number. Therefore, there are no real roots for the given quadratic part. We have arrived at the same conclusion that we reached graphically.

Graphing Quadratic Equations in Vertex Form

The vertex course of a quadratic function lets its vertex be found hands.

Learning Objectives

Explain the meanings of the constants [latex]a[/latex], [latex]h[/latex], and [latex]k[/latex] for a quadratic equation in vertex form

Cardinal Takeaways

Key Points

• An of import grade of a quadratic function is vertex class: [latex]f(x) = a(10-h)^2 + k[/latex]
• When written in vertex course, information technology is easy to run across the vertex of the parabola at [latex](h, k)[/latex].
• Information technology is easy to catechumen from vertex course to standard form.
• Information technology is more difficult, but withal possible, to convert from standard class to vertex class. The procedure involves a technique called completing the square.

Key Terms

• constant: An identifier that is bound to an invariant value.
• vertex: A bespeak on the bend with a local minimum or maximum of curvature.
• quadratic: A polynomial of degree 2.

Quadratic equations may take various forms. You have already seen the standard form:

[latex]f(10)=a{ x }^{ two }+bx+c[/latex]

Some other common class is called vertex form, because when a quadratic is written in this class, it is very easy to tell where its vertex is located. The vertex form is given by:

[latex]f(x)=a(x-h)^2+k[/latex]

The vertex is [latex](h,k).[/latex] Note that if the form were [latex]f(x)=a(x+h)^ii+one thousand[/latex], the vertex would be [latex](-h,k).[/latex] The coefficient [latex]a[/latex] as before controls whether the parabola opens up or down, as well equally the speed of increase or decrease of the parabola.

Converting From Vertex Course to Standard Form

If you want to convert a quadratic in vertex form to one in standard form, only multiply out the square and combine similar terms. For case, the quadratic

[latex]y=(ten-2)^2+ane[/latex]

Can be rewritten every bit follows:

[latex]\begin{align} y&=(ten-2)(x-2)+1 \\ &=ten^2-2x-2x+4+1 \\ &=10^2-4x+5 \end{align}[/latex]

Converting From Standard Form to Vertex Course

It is more difficult to convert from standard course to vertex course. The procedure is called "completing the square."

Conversion When [latex]a=1[/latex]

Consider the following instance: suppose you desire to write [latex]y=x^2+4x+6[/latex] in vertex class. Note that the coefficient on [latex]10^2[/latex] (the one we call [latex]a[/latex]) is [latex]1[/latex]. When this is the case, we await at the coefficient on [latex]x[/latex] (the one nosotros call [latex]b[/latex]) and take one-half of information technology. Then we square that number. Thus for this example, we split [latex]4[/latex] by [latex]two[/latex] to obtain [latex]2[/latex] and then square it to obtain [latex]4[/latex].

Nosotros so both add and subtract this number as follows:

[latex]y=(ten^2+4x+four)+6-4[/latex]

Note that nosotros both added and subtracted iv, so we didn't actually change our office. At present the expression in the parentheses is a square; nosotros tin write [latex]y=(x+2)^2+2.[/latex] Our equation is now in vertex form and nosotros can see that the vertex is [latex](-2,two).[/latex]

Conversion When [latex]a \neq 1[/latex]

It is slightly more complicated to convert standard form to vertex course when the coefficient [latex]a[/latex] is not equal to [latex]one[/latex]. We tin can nonetheless use the technique, simply must be careful to start factor out the [latex]a[/latex] equally in the following case:

Consider [latex]y=2x^2+12x+5. [/latex] We factor out the coefficient [latex]2[/latex] from the first two terms, writing this as:

[latex]y=2(x^ii+6x) + 5[/latex]

We then complete the square inside the parentheses. Note that one-half of [latex]6[/latex] is [latex]3[/latex] and [latex]three^ii=9[/latex]. So we add and decrease [latex]ix[/latex] inside the parentheses, obtaining:

[latex]y=2(x^2+6x+9-9)+5[/latex]

We can then finish the calculation every bit follows:

[latex]\begin{align} y&=ii((ten+iii)^2-9)+5 \\ &=ii(x+three)^2-xviii+5 \\ &=(10+3)^2-xiii \finish{align}[/latex]

So the vertex of this parabola is [latex](-3,-13).[/latex]

Graphing Quadratic Equations In Standard Course

A quadratic function is a polynomial function of the form [latex]y=ax^2+bx+c[/latex].

Learning Objectives

Explain the meanings of the constants [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] for a quadratic equation in standard form

Key Takeaways

Key Points

• The graph of a quadratic role is a parabola whose axis of symmetry is parallel to the [latex]y[/latex]-axis.
• The coefficients [latex]a, b,[/latex] and [latex]c[/latex] in the equation [latex]y=ax^ii+bx+c[/latex] control diverse facets of what the parabola looks like when graphed.

Key Terms

• vertex: The maximum or minimum of a quadratic function.
• parabola: The shape formed by the graph of a quadratic function.
• quadratic: A polynomial of degree two.

A quadratic function in the form

[latex]f(10)=a{ x }^{ ii }+bx+ten[/latex]

is in standard grade.

Regardless of the format, the graph of a quadratic function is a parabola.

The graph of [latex]y=x^2-4x+3[/latex] : The graph of whatever quadratic equation is always a parabola.

Coefficients and Graphs of Quadratic Role

Each coefficient in a quadratic function in standard grade has an impact on the shape and placement of the function's graph.

Coefficient of [latex]x^2[/latex], [latex]a[/latex]

The coefficient [latex]a[/latex] controls the speed of increase (or decrease) of the quadratic function from the vertex. A larger, positive [latex]a[/latex] makes the function increase faster and the graph appear thinner.

The coefficient [latex]a[/latex] controls the speed of increment of the parabola.: The black curve is [latex]y=4x^ii[/latex] while the blue curve is [latex]y=3x^ii.[/latex] The black bend appears thinner because its coefficient [latex]a[/latex] is bigger than that of the blue curve.

Whether the parabola opens upward or downwards is likewise controlled by [latex]a[/latex]. If the coefficient [latex]a>0[/latex], the parabola opens upward, and if the coefficient [latex]a<0[/latex], the parabola opens downward.

Quadratics either open upwards or downwardly: The blueish parabola is the graph of [latex]y=3x^2.[/latex] It opens upward since [latex]a=three>0.[/latex] The black parabola is the graph of [latex]y=-3x^2.[/latex] It opens downwards since [latex]a=-3<0.[/latex].

The Axis of Symmetry

The coefficients [latex]b[/latex] and [latex]a[/latex] together control the axis of symmetry of the parabola and the [latex]10[/latex]-coordinate of the vertex. The axis of symmetry for a parabola is given by:

[latex]x=-\dfrac{b}{2a}[/latex]

For example, consider the parabola [latex]y=2x^2-4x+4 [/latex] shown below. Because [latex]a=two[/latex] and [latex]b=-4,[/latex] the centrality of symmetry is:

[latex]x=-\frac{-4}{2\cdot 2} = 1[/latex]

The vertex besides has [latex]x[/latex] coordinate [latex]1[/latex].

The graph of [latex]y=2x^ii-4x+iv.[/latex]: The axis of symmetry is a vertical line parallel to the y-axis at  [latex]x=1[/latex].

The [latex]y[/latex]-intercept of the Parabola

The coefficient [latex]c[/latex] controls the height of the parabola. More specifically, it is the point where the parabola intercepts the y-axis. The point [latex](0,c)[/latex] is the [latex]y[/latex] intercept of the parabola. Notation that the parabola above has [latex]c=four[/latex] and it intercepts the [latex]y[/latex]-axis at the point [latex](0,iv).[/latex]

Source: https://courses.lumenlearning.com/boundless-algebra/chapter/graphs-of-quadratic-functions/

Posted by: madsensels1994.blogspot.com

Share this post